AI, the Bible, and our Future
1.3 The Neural Network
image generated with Ideogram 1.0 on ideogram.ai
Introduction into Artificial Neural Networks
While the perceptron (as explained in my last section 1.2 The Perceptron) models a single neuron in the brain, an Artificial Neural Network (ANN) is instead comparable to a whole network of neurons—hence, Network. I will use the terms "Neural Network" and "Artificial Neural Network" interchangeably.
Neural networks can vary greatly in size, measured by the number of parameters (weights and biases) they contain. This can range from hundreds to trillions of parameters! The amount of parameters determines the network's complexity and capacity to learn patterns that are present in the training data. The weights, as explained with the perceptron, determine the importance of the input a neuron receives, while the bias is adding another layer of complexity to the neural network to learn the training data.
"Neural Network" is actually an umbrella term referring to many different types of neural network architectures, each with its own working mechanisms and use cases. Here is a broad overview:
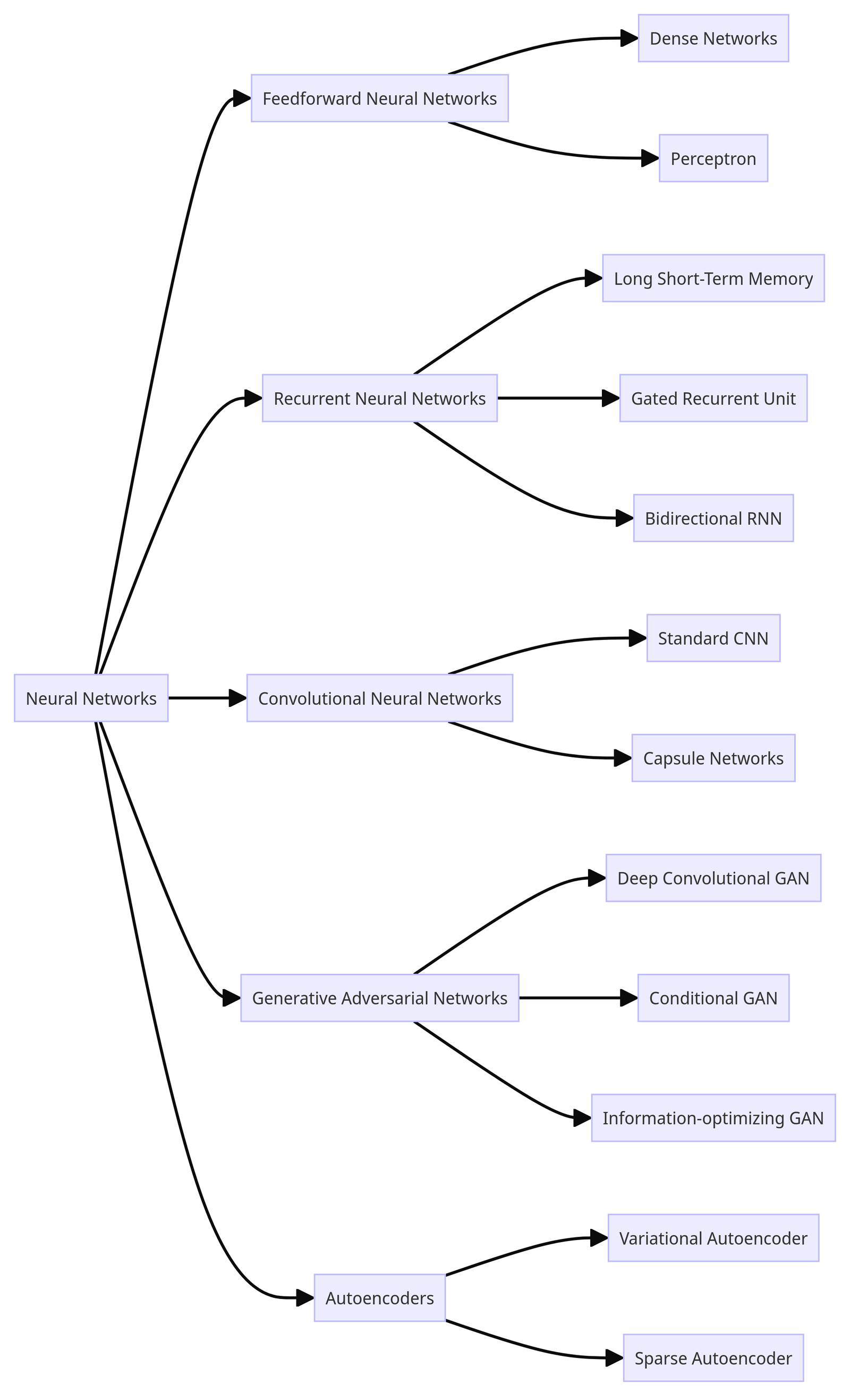
As you can see, there are a great variety of neural networks. To stay within the context of interactive AI chatbots (such as ChatGPT), we will only focus on the Feedforward Neural Network (FNN), specifically the Dense Network (also known as the Fully Connected Neural Network or Multilayer Perceptron).
The FNN is comprised of a huge amount of "perceptron-neurons." If you haven't yet, I highly recommend reading the previous section 1.2 The Perceptron, as it will give you the necessary foundation for understanding the FNN we will talk about now.
In a feedforward neural network, information is processed from the input layer through the hidden layers to the output layer without any loops. The information only moves "forward" through the NN. The dense network is so named because each neuron in a given layer is connected to every neuron in the subsequent layer, hence the names "dense" or "fully connected."
Structure of a Feedforward Neural Network
Instead of the umbrella example in 1.2 The Perceptron, we will use the much more complex (and actually useful) example of recognizing a drawn number between 0 and 9 on a 28 × 28 grid.
The Input Layer
First, we need to think about how an image can be represented in numbers, as a neural network can only work with numerical values. For that, we will just use one feature for each pixel and use the grayscale value of each pixel as the input.
We have 28 × 28 = 784 pixels and therefore 784 input features. In the input layer you have features and not neurons, because neurons are the processing units that perform computations on the input data. The input layer, as opposed to the other layers, simply holds the raw input values without performing any calculations. The grayscale value will be between 0 and 1, with 0 being white and 1 being black. 0.5 would be a perfect gray. As you can see, those are already a lot more input features compared to the three we had with the perceptron!
The Hidden Layers
This is where all the magic of artificial intelligence happens (or should I say it's where all the math happens?!) and where the neural network learns complex patterns. There is technically no limit in how many hidden layers you can have, but sometimes less is more. Those hidden layers extract patterns from the training data with the goal to then recognize those learned patterns in a given input image. Think about how you would recognize a number. You might look for circles and strokes. The number "8", for example, has one circle on another circle, while the "1" has one vertical stroke and a short diagonal one coming from the top of the first stroke and going down to the left. If those patterns would be learned correctly during training (even if we are not aware of them), AI would be able to achieve human-level, or even superhuman performance!
This is also where the similarity to the perceptron lies. Each neuron in the hidden layer will receive the inputs from each neuron in the previous layer (the input layer in this case), calculate the weighted sum, add a bias, and apply an activation function before the output is passed to the next layer. That is why this specific FNN is also called a Multilayer-Perceptron. Each neuron in the hidden layers is a perceptron!
If there would be 16 patterns that could be found in the numbers 0-9, it would be best to have a hidden layer with 16 neurons. Then, you could add another layer for recognizing subparts of those patterns, again, optimally with an amount of neurons corresponding to the amount of sub-patterns that are existing.
If the FNN gets an image with the number "9" as the input, the neural network could recognize the circle on top of a line bending to the left. The neurons that hold the information for those patterns would have a high activation, which would result in a high activation of the output neuron that holds the information for the number "9".
In reality, though, the neural networks don't always capture patterns as we would expect them to do. This is what makes the creation of neural networks actually hard: building them in a way that can most optimally hold (or "save") the information from the training data.
The Output Layer
In the output layer, 10 neurons are needed to represent the full range of ten possible numbers as the output (numbers 0-9). Each neuron in this layer is, again, a perceptron: receiving inputs from the hidden layer, calculating the weighted sum, adding a bias, and applying an activation function. In our case, we would use the Sigmoid activation function which provides us a number that can be interpreted as a percentage. After the patterns are recognized in the hidden layers, some of those neurons get activated more than others. The neuron in the output layer for the number "9" might get the result of 0.9, which means a probability of 90% that the input number was a "9" indeed.
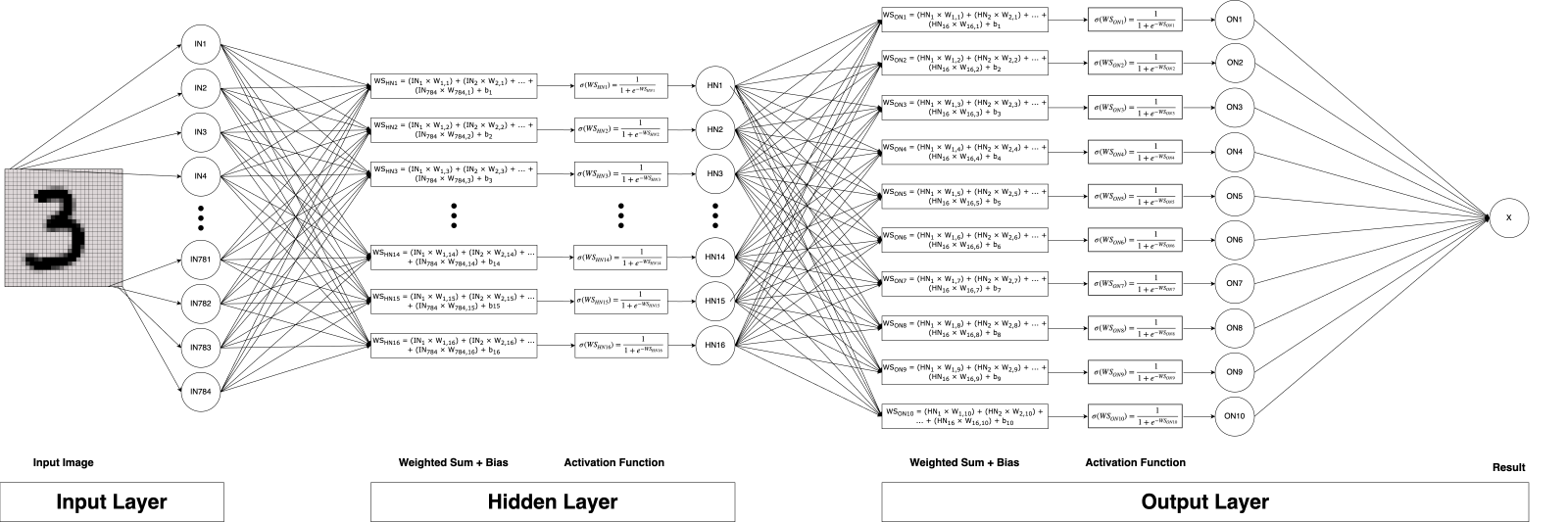
Figure 2: Representation of a Multilayer Perceptron. The input image is given in the input layer. The gray values for each pixel sum up to 784 features. In the hidden layer, the weighted sum is calculated, a bias is added, and the Sigmoid activation function is applied for all 16 neurons. The result will be passed on to the output layer in which, again, for each of the 10 neurons, the weighted sum is calculated, the bias is added, and the Sigmoid activation function is applied. In the last step, the neuron with the highest activation is considered to be the number given in the input image.
Example of a Complete Function
A neural network is essentially a highly complex composite function. A composite function is a function composed of two or more functions, where the output of one function becomes the input for the next. This composite function is then applied to a given input vector X. The result of applying the function to a neuron or a layer of neurons is called the activation. However, we not only want to calculate the individual activations but also the entire network's output (prediction). The example with the input on a 28 × 28 grid is too large to fully write down, so let's consider a simpler, smaller example through which we can gain a complete understanding of what happens inside the neural network:
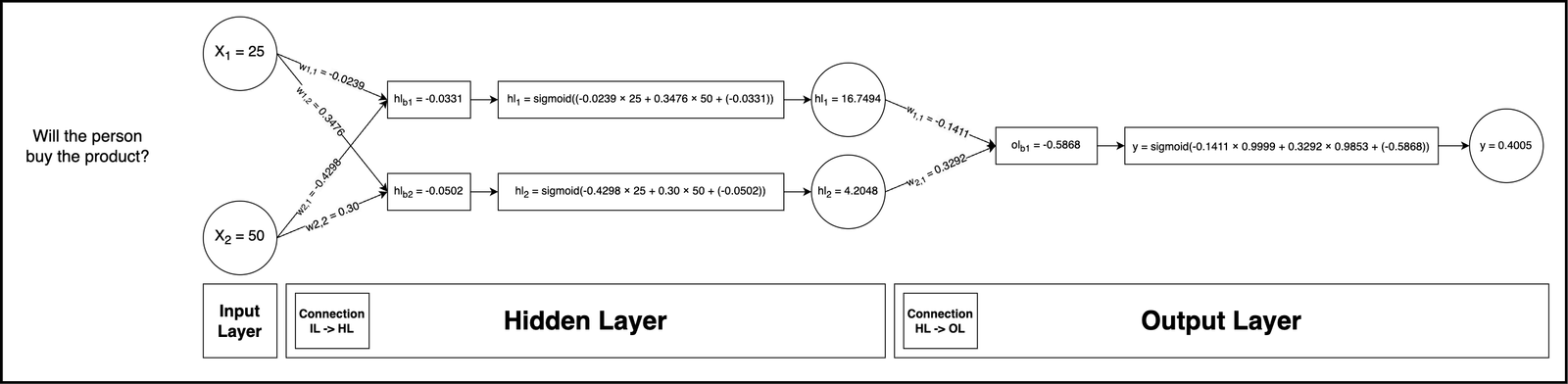
Consider the prediction of whether a person will buy a product based on just their age and annual income. These are our two input features. For the hidden layer, we will have two neurons, and one neuron for the output layer. Overall, this neural network is composed of 3 Neurons.
For calculating the parameters, we have:
2 × 2 + 2for the weights from the input layer to the hidden layer plus the biases for the two neurons in the hidden layer.2 × 1 + 1for the weights from the two hidden neurons to the output neuron plus the bias for the output neuron.
That sums up to a neural network with 9 Parameters.
Input Data:
- Age: 25 (years)
- Annual Income: 50 (thousand dollars)
Weights & Biases:
I asked GPT-4o to write the code for training a small neural network using PyTorch. GPT-4o then created a logic for determining when a person would buy a product and generated adequate training data to ensure the NN's convergence. After 200 epochs, the NN achieved a loss of 0.6020, which is a relatively good result for my use case. The loss indicates how well the NN converged, with values closer to zero being more desirable. An epoch refers to the NN processing the entire dataset once. For small datasets like the one used in this case, the number of epochs typically ranges between 100 and 1000. The following are the actual weights and biases learned by the NN during the training process:
w1,1 = -0.0239w1,2 = 0.3476w2,1 = -0.4298w2,2 = 0.30hlb1 = -0.0331;hlb2 = -0.0502
w1,1 = -0.1411w2,1 = 0.3292olb1 = -0.5868
General Structure
The composite function of this NN is made up of two separate functions, which I will mark with distinct colors for clarity:
- Input Layer to Hidden Layer:
Xas the input.W1as the weights for the connections from the input layer to the hidden layer.b1as the biases for the hidden layer.σ1(Sigma) as the activation function for the hidden layer.
The output of the hidden layer,
H1, can be expressed as:H1 = σ1(W1 × X + b1) - Hidden Layer to Output Layer:
W2as the weights from the hidden layer to the output layer.b2as the biases for the output layer.σ2as the activation function for the output layer.The output of the network,
y, can be expressed as:y = σ2(W2 × H1 + b2)
By combining the two above functions, we have the following composite function:
y(X) = σ2(W2 × σ1(W1 × X + b1) + b2)Calculation:
Before we dive into the calculations, let's remember the basics of vectors and matrices, and how to multiply them.
A vector is a one-dimensional array of numbers, represented using square brackets. For example:
v = [1, 2, 3]A matrix is a two-dimensional array of numbers, also represented using square brackets. For example:
M = [[1, 2],
[3, 4],
[5, 6]]To multiply a matrix by a vector, the number of columns in the matrix must equal the number of rows in the vector. The resulting vector will have the same number of rows as the matrix has columns. Each element in the resulting vector is calculated by multiplying the corresponding row of the matrix by the vector and summing the results. I recommend taking a look at http://matrixmultiplication.xyz as it makes it a lot easier to understand how matrixmultiplication works. Mathematically, this is expressed as:
(M × v)i = Σj Mi,j × vjIn this expression:
(M × v)represents the resulting vector from the matrix-vector multiplication.iis the index of the row in the resulting vector.Σ(sigma) denotes the summation operation.jis the index that runs through the columns of the matrix and the elements of the vector.Mi,jrepresents the element at the i-th row and j-th column of the matrix M.vjrepresents the j-th element of the vector v.
In other words, to calculate the i-th element of the resulting vector, we multiply each element in the i-th row of the matrix by the corresponding element in the vector and sum up the results.
Let's fill in the calculation for the actual numbers we have, using the matrix-vector multiplication formula:
(M × v)i = Σj Mi,j × vjIn our example, the input vector is:
X = [25, 50]The weight matrix for the hidden layer is:
W1 = [[W1,1, W1,2], [W2,1, W2,2]]W1 = [[-0.0239, 0.3476], [-0.4298, 0.30]]
To calculate the matrix-vector multiplication W1 × X, we apply the formula for each row of the matrix:
(W1 × X)1 = Σj W1,j × Xj
= W1,1 × X1 + W1,2 × X2
= -0.0239 × 25 + 0.3476 × 50
= 16.7825
(W1 × X)2 = Σj W2,j × Xj
= W2,1 × X1 + W2,2 × X2
= -0.4298 × 25 + 0.30 × 50
= 4.255So, the result of the matrix-vector multiplication is:
W1 × X = [16.7825, 4.255]Now, we can proceed with the rest of the calculation for the hidden layer activation:
H1 = σ1(W1 × X + b1)
= σ1([16.7825, 4.255] + [-0.0331, -0.0502])
= σ1([16.7825 + (-0.0331), 4.255 + (-0.0502)])
= σ1([16.7494, 4.2048])Using the sigmoid activation function σ1, we have the formula:
σ(x) = 1 / (1 + e-x)We can calculate the activations of the two hidden layer neurons:
H1 = [σ(16.7494), σ(4.2048)]
= [0.9999, 0.9853]Now, let's calculate the output layer activation using the hidden layer output, weights, and biases:
y = σ2(W2 × H1 + b2)The weight matrix for the output layer is:
W2 = [[W1,1], [W2,1]]W2 = [[-0.1411], [0.3292]]
To calculate the matrix-vector multiplication W2 × H1, we apply the formula:
(W2 × H1)1 = Σj W1,j × H1,j
= W1,1 × H1,1 + W2,1 × H1,2
= -0.1411 × 0.9999 + 0.3292 × 0.9853
= 0.1833Now, we can proceed with the rest of the calculation for the output layer activation:
y = σ2(W2 × H1 + b2)
= σ2(0.1833 + (-0.5868))
= σ2(-0.4035)Using the sigmoid activation function σ2, we have:
y = σ(-0.4035)
= 1 / (1 + e0.4035)
= 0.4005Therefore, the output of the neural network for the given input [25, 50] is 0.4005, which can be interpreted as a 40.05% probability that the person will buy the product. And that's it, we just calculated the inner workings of a FNN by hand!
This part of the process can be mathematically hard to comprehend, but it gives you a clear picture of what is actually happening. It took a great amount of time to figure it all out myself. Take your time to read through it again. Think about it and maybe even try to use different inputs for the calculation!
While the example we used is relatively simple, it still applies to a dense NN of any size.
For this book project, I will not go into the math of how neural networks learn from training data, but now it should make a lot more sense that, during that process, the weights and biases are simply updated to predict the training dataset more accurately.