1.2 The Perceptron – AI and the Bible

image generated with Ideogram 1.0 on ideogram.ai

Blog Post Template

Last Updated: 13-Aug-24

The Perceptron, the simplest form of a neural network.

Introduced in the report The Perceptron: A Perceiving and Recognizing Automaton in 1957, the perceptron depicts the workings of a single neuron in the brain. It takes input signals, processes them, and produces an output signal which must be binary (On or Off; 0 or 1; white or black; pen or paper; it can really be anything).

Let's consider a perceptron that is supposed to tell us if we should take an umbrella with us when going outside or not. In this case, the output might be "Yes" or "No", though I used the booleans (a datatype for truth values) TRUE or FALSE in Figure 1.

The Input

The perceptron consists of four components, the first being the Input Layer.

The Input Layer is whatever the perceptron is given to classify or compute. In our example, it is the current weather, the weather forecast, and the season. Each of those three factors is needed for the perceptron to generate a relevant output. In our example (as seen in Figure 1), I use numbers instead of words to represent the state of the three inputs because words cannot be used in an equation.

We have the following options for the input, though it could easily be extended:

Current Weather: Sunny (0), Cloudy (0.5), Rainy (1)
Weather Forecast: Sunny (0), Cloudy (0.5), Rainy (1)
Season: Summer (1), Winter (0)

Let's assume it is raining at the moment, the weather forecast is cloudy weather, and it is winter. We therefore have the inputs W=1; F=0.5; S=0.

Weighted Sum

The second component of the perceptron is the weighted sum. Every input in the input layer has a so-called weight. The weight determines the importance of the input. In our example, the most important factor is, of course, the current weather which I assigned a weight of 0.5, following with the weather forecast with a weight of 0.3, and lastly the season with a weight of 0.2. In an actual perceptron, we would start with random weights and the perceptron would learn the words through an algorithm. We will get to the training process later in this post.

For the weighted sum, we are simply multiplying each input (X) with its corresponding weight (W) and then adding them together:

(X₁ × W₁) + (X₂ × W₂) + (X₃ × W₃)

If we fill in the actual numbers:

(1 × 0.5) + (0.5 × 0.3) + (0 × 0.2) = 0.65

Activation Function

Now, it's time to transform the weighted sum into a usable output. That's the job of the activation function, the third component of the perceptron. If you remember, the output of a perceptron can only be binary.

In the case of a perceptron, we commonly use the Heaviside step function as the activation function. This function can be visualized as a step on a staircase, hence the name step function.

Imagine a staircase with two levels: a lower level and an upper level. The Heaviside step function behaves like this staircase. Instead of a gradual increase, the function jumps directly from the lower level to the upper level at a specific point, called the threshold.

Mathematically, the Heaviside step function is defined as follows:

If the input is less than the threshold, the function outputs the lower level (in our case 0, or FALSE).
If the input is greater than or equal to the threshold, the function outputs the upper level (in our case 1, or TRUE).

Our perceptron has a threshold of 0.5. Our weighted sum (0.65) is greater than 0.5, and therefore, the activation function transforms the weighted sum to the full number "1". This result comprises the fourth and final component of the perceptron—the output layer.

Output Layer

As the name already suggests, this is the component in which we finally get the answer if we should take an umbrella or not! The output layer simply is the result of the calculations. In the example in Figure 1, the result is that we should take an umbrella with us.

This particular example is rather simple using only three inputs, but the perceptron has the capacity to process any number of inputs. It is also capable of processing any input that can be represented by a number. This ability of the perceptron allows it to recognize or differente between shapes, such as a circle and a rectangle. Frank Rosenblatt defined perceptrons as follows:

"The proposed system depends on probabilistic rather than deterministic principles for its operation, and gains its reliability from the properties of statistical measurements obtained from large populations of elements. A system which operates according to these principles will be called a perceptron."
Rosenblatt, F. (1957). The Perceptron: A Perceiving and Recognizing Automaton (Project PARA). Cornell Aeronautical Laboratory Report No. 85-460-1. Buffalo, NY: Cornell Aeronautical Laboratory. p. 2.

Frank Rosenblatt is comparing the usage of a perceptron to the usage of any rule-based program (deterministic system). In a rule-based program, the input is compared to a list of examples. If a match is found in those examples, the shape can be clearly recognized. However, in a perceptron (a probabilistic system), the examples are the training data that will teach the perceptron what a circle or rectangle looks like. It can then make a prediction of whether the shape is more circular or rectangular.

There you see the difference in the amount of computation needed. In the deterministic system, the input must be compared to all the examples which would never guarantee that a match is found (especially not for hand drawn shapes). These examples are no longer necessary with the use of the perceptron because the examples are used to train the perceptron, which will then be a representation of all the examples.

Training a Perceptron

Now that we have looked at the four components of a perceptron, let us train one ourselves!

There are only two conditions:

The input data must be linearly separable.
The output data must be binary.

We already clarified what a binary output means, but what is linear separability?

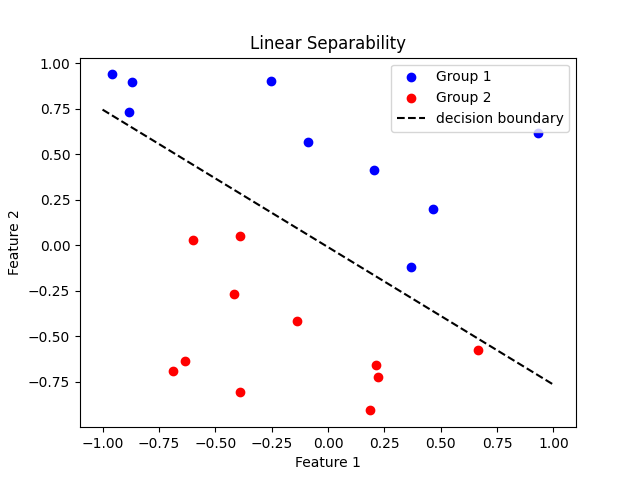
Linear Separability means that two groups of datapoints can be separated through a straight line or hyperplane (separation through any amount of dimensions) which is called the decision boundary. This is best visualized on a 2D graph as seen below. Group 1 is blue, and Group 2 is red. They can be separated by a straight line.

Finally, let's dive into the training process, which involves the following steps:

Initialize the weights: We start by assigning random values to the weights of the perceptron. These initial weights will be adjusted during the training process.
Feed the input data: We provide the perceptron with a set of input data, along with the corresponding desired output (also known as the target or label). In our umbrella example, we would feed the perceptron with various combinations of current weather, weather forecast, and season, along with the correct answer of whether an umbrella is needed or not.
Calculate the predicted output: For each input data point, the perceptron calculates the weighted sum of the inputs and applies the activation function (Heaviside step function) to determine the predicted output. This is the same process we discussed earlier.
Compare the predicted output with the desired output: The perceptron compares its predicted output with the desired output provided in the training data. If the predicted output matches the desired output, the perceptron has made a correct prediction. However, if there is a mismatch, the weights of the perceptron must be adjusted.
Update the weights: If the predicted output differs from the desired output, the weights in the perceptron are updated to minimize the error and can therefore correctly predict if an umbrella is needed or not. The weight update is performed using the perceptron learning rule:
- If the perceptron predicts 0 (FALSE) but the desired output is 1 (TRUE), the weights are increased by a small amount proportional to the corresponding input values.
- If the perceptron predicts 1 (TRUE) but the desired output is 0 (FALSE), the weights are decreased by a small amount proportional to the corresponding input values.
The amount by which the weights are adjusted is controlled by a parameter called the learning rate, which determines the step size of the weight updates. Look at Figure 2 again, and imagine that the decision boundary was not found. The line starts at a random position, so a few of the datapoints are not correctly separated. When updating the weights, the decision boundary is moved and tilted a little bit.
Repeat the process: Steps 2-5 are repeated for each input data point in the training set, and the process is iteratively performed for a specified number of epochs (complete passes through the training data) or until the perceptron converges and makes accurate predictions (i.e. the line successfully separates the two groups of datapoints). At this point, the perceptron has learned the training data.

Through this training process, the weights of the perceptron are adjusted in a way that minimizes the errors and enables it to make accurate predictions on new, unseen data. The perceptron learning rule ensures that the weights are updated in the direction that reduces the discrepancy between the predicted output and the desired output. If the training data would not be linearly separable, the perceptron would not be able to make accurate predictions.

Below, I have plotted an example of what a few datapoints might look like for our perceptron that should predict the need of an umbrella. As you can see, all datapoints are separated into two groups, and the perceptron can now make accurate predictions. There could always be a new datapoint which does not fit, though the probability of this happening reduces by having a greater amount of training data.

Figure 3: 3D plot of the perceptron which predicts the need of an umbrella. The decision boundary shows that the training data was correctly learned.

In the next section, 1.3 The Neural Network, we will introduce a few more concepts that will get us a step closer to understanding large language models like ChatGPT. This will also give us the basic framework necessary to understand how an AI was able to acknowledge the existence of the God of the Bible (AI Acknowledges Existence of Yahweh).

Subscribe below if you would like to receive my newsletter with updates on posts and the blog!

Sources & Further Reading:

Some ideas and information for this blog post were generated with the help of Claude-3-Sonnet and Claude-3-Opus, AI assistants developed by Anthropic. While Claude offered valuable suggestions and explanations, the content presented here is the author's own work.